Search the Community

But I again emphasize that a lot of science is not done statistically at all. Even though I think in medical science it is more common. And no one compute a correlation coefficient. Look through a telescope and see a sunspot and refuse to say there is a solar flare going on because I forgot to compute the correlation for the event. Run navier stokes equation in a computational fluid dynamics estimate for air flow over a wing and refuse to interpret the results since this is only one data point and so I can't compute a correlation. Tell you what- your comfort with making important decisions with incomplete information, in crisis moments - as a medical professional - your my kinda guy and I only hope I would have you on call if I ever need you!!!

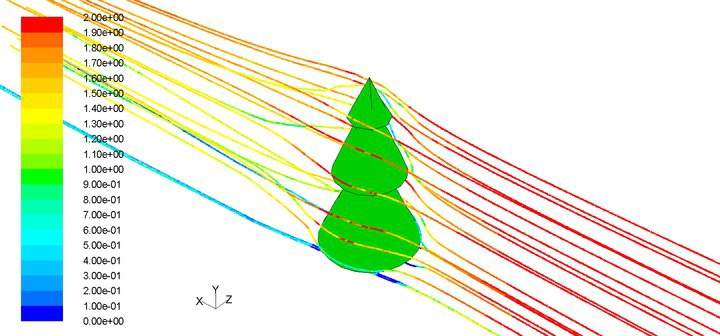
Pilots are fascinated with lift -- it keeps us aloft. But, its origin is somewhat mysterious. On one hand, there are the Navier-Stokes equations used by engineers that accurately describe the behavior of fluids in motion and allow prediction of aerodynamic forces, but do not provide much physical insight. On the other hand, there are the popular explanations invoking Bernoulli and Newton that are easy to visualize but incomplete or inaccurate. There are a lot of videos on youtube (some by college professors) that are just wrong. But, here's a very good one that offers a reasonable physical description without the pitfalls created by oversimplification. Skip

Ahhhh... (way cool!) Mr.(s) Navier and Stokes have visited here before... https://mooneyspace.com/search/?q=Navier&quick=1 We have a few people around MS that are familiar with both the fluid flow and the math... Best regards, -a-

@carusoam The flat plates metaphor is a good one. Communicates the converging wedge idea well. The dominant equation is "Reynolds Equation" which is a simplified version of Navier Stokes for fluid flow. Over 100 years and the math still works :-) My work is actually with bearings that work with air (we design and make air foil bearings), but I started with gas turbines using conventional oil lubricated bearings. Like any topic, the more you dig, the more there is to learn.

We have voiced all of our opinions, but no one has changed their minds … typical pilot conversation (I am one, too). BUT ... 1. We have good CFD models that predict lift, drag and pitching moment well … most of the time. We pay good aerodynamicists to know when the CFD is right or wrong. These CFD programs also include boundary layer (and millions of panels or nodes). Typically, the equations involve full Navier-Stokes equations, which include Bernoulli and Newton. 2. If you believe a typical Mooney wing has laminar flow further aft than other airplanes, I have ocean-front property for you in Arizona. Sorry. Please note that there are basically 3 types of boundary layer flow (boundary layer is the flow close to the surface and measured perpendicular to the surface until the flow velocity becomes free stream. It starts at 0" thickness at the stagnation point and grows until it is ~1/2" thick at the trailing edge. 3. The SAME airfoil cross section will perform differently at different Reynold numbers. This is an area that separates the engineers from the pilots (innuendo intentional). If the root chord is 72" and the tip chord is 36", the tip airfoil will stall first (the Rn of the root is 2X the tip). If an airplane is flying at a higher speed and/or higher altitude, it will stall at a higher AOA because the Rn is hgher. The Cd of a Pilates ball (smooth, large diameter) is lower than a ping pong ball (smooth small diameter because the Rn is higher on the big ball. This is why smaller, round antenna produce more drag than a larger, streamlined antenna. 4. A golf ball is dimpled because … okay, I've gone to far.

Yes, density is constant in Bernoulli equations but you can re-write similar equations for compressible fluids on laminar airflow cross-sections (shockwaves surface are where density kinks), the maths are very easy to workout as you can still draw airflow cross-sections with similar physical properties, the only non-intuitive thing passing Mach >1 is that the section has to diverge for airflow to accelerate, so you have throw Mr Venturi to the bin and build parabolic nozzles The main issue is that to analytically calculate and understand the physical properties of the airflow you need to know the airflow lines, cross-sections, stagnation/separation points and boundary layers...that gets messy for turbulent airflows, although you can still apply Bernoulli style equations with dissipative terms but you will have a really hard time doing constant energy physics on fractals (turbulence from a 2D wing do lives in 2.89 dimensions ) For theory, you can just draw a wing and some airflow and walk-through some very simplified 2D equations or analogies, in practice, we only know the airflow speed/pressure at the start and end of that big wind tunnel Of course you can run Navier-Stokes equations on a super computer and check accuracy versus analytical solution on simple cases or empirical results on reduced models When I used to work on these, I recall one did miserably failed while the other one seemed to work well, I let you guess which one?

Sorry, all. I haven't listened to Rod's video yet, but I am an aerodynamicist. I'll get to Rod's video later this evening. In very simple terms everyone has made true statements (and the contrary is true, too). Bernoulli cannot explain 100% of lift generation nor can Newton. They are both utilized in the Navier-Stokes equations that used to be computed by hand, but are now imbedded in CFD programs. For real CFD simulation, the boundary layer also has to be modeled. There are also good CFD programs that model well enough to run loads programs and the like. Some of the good programs will model the separation point, but programs are getting better (but not there yet) on modeling the flow (and boundary layer) after separation. Now, for popular misconceptions. #1 Air flow does not hit the physical "leading edge" of the airfoil. Remembering that the wing is twisted (every span-wise local AOA is different), we'll simplify to 2D and look at a single span-wise location (say at the stall warning switch). So, looking at a 2D airfoil, the air "hits" the airfoil below and aft of the leading edge at a point called the stagnation point. The stagnation point is where the air hits the airfoil and stops (in a perfect computer world). Air flow above the stagnation streamline (yes, there is upwash before the wing … and propeller) flows forward and around the top of the airfoil, and air flow below the stagnation streamline flows along the bottom of the airfoil. The upper surface particles don't move faster because they know it's a longer distance. They travel faster because they are pulled faster by a lower pressure. The stall warning horn activates when the stagnation point is aft of the vane, and the forward moving air flow pushes the flipper up into the contacts inside the switch. Brutally simple #2 (depending on AOA) Static air pressures on the bottom of the airfoil are not higher than ambient pressure. At low AOAs the majority of the bottom of the airfoil is also below static ambient pressure. They are higher than static pressures on the top of the airfoil, though. It is this delta P that creates lift. #3 Camber (curvature) is not required to create lift. Note: the second video has a lot of errors in it. The "curvature" (shape of the mean camber line) is a large factor in the efficiency of the airfoil. The straight slope of Cl vs. AOA curves is the flat plate lift of the airfoil. Note: airfoil design is complicated. Time to take a breath. Great thread. -Ron

You amateur aerospace engineers are so adorable... The forces acting on an object moving through a fluid are definitely more complicated than any of the simplified algebraic equations you are posting. Most of what you are posting is simplified versions of a difficult triple integral problem that describes the conservation of momentum in a viscous compressible fluid -- if you make simplifying assumptions about shape, viscosity, and compressibility, you get to each equation you are debating. None of which perfectly describes the forces acting on an wing, let alone the whole aircraft (see navier stokes equation) alone. Fwiw, neither does Bernoulli, to get to his equation, you also have to make simplifying assumption that does not take into account spanwise lift, amongst other things, for instance, but it is also derived from the conservation of momentum equations. But Bernoulli's equations are derivable form Newton's Laws, it's not either or, it's just an expression of conservation of momentum. So, given that and the title of the thread, I vote Newton's Laws win. as for how to teach a student pilot without calculus, I think basic constructs of force vectors and effect of angle of attack on lift seems to do the job. Don't change what works. I can tell you from experience lots of pilots are startlingly bad at math. (BS Aerospace Engineering, Georgia Tech; Masters Mechanical Engineering, Rice University. Happy to send anyone copies of my text books and fluid dynamics notes, if anyone wants to learn the governing equations themselves.)